Why the Monty Hall Problem Still Fools Us: Cognitive Bias and the Illusion of Rational Choice

By Leandro Castelluccio

The Monty Hall Problem and the Art of Overthinking

We rarely notice how our habit of dividing, classifying, and overanalyzing distorts our grasp of the obvious. One of the clearest illustrations of this tendency appears in an unlikely place: a simple probability game known as the Monty Hall problem.

The Monty Hall problem is famous because it challenges intuition. At first glance, the correct answer seems absurd—so absurd, in fact, that even mathematicians have publicly doubted it. The problem underscores a broader cognitive pattern: we often let complexity obscure the truth. This post explores how our intellectual instinct to segment and analyze can lead us away from simple, correct conclusions.

The Setup: A Game of Doors and Decisions

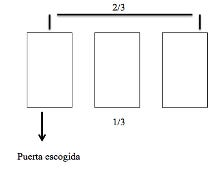
Imagine a game show with three closed doors. Behind one is a car; behind the other two, goats. You pick one door. The host, who knows what lies behind each, opens one of the other two doors—always revealing a goat. You’re then asked: stick with your original choice, or switch to the remaining unopened door?

Statistically, the optimal strategy is to always switch. Why? When you choose your initial door, the chance that it hides the car is 1 in 3. That leaves a 2 in 3 chance the car is behind one of the other two doors. When the host opens one of those doors to reveal a goat, he’s giving you information—essentially condensing that 2/3 chance onto the single remaining unopened door.

By switching, you’re choosing the 2/3 probability; by staying, you cling to the 1/3. It’s a non-intuitive insight that continues to spark debate decades after the problem gained popularity.

The Cognitive Trap: Fragmented Reasoning

Here’s where the mind complicates things. Suppose you initially choose Door 1. You might then reason: “The car is either behind Door 1 or Door 2—that’s two out of three possibilities.” If the host opens Door 2 to reveal a goat, you might falsely conclude that Door 1 now has a higher chance.

But this ignores a key fact: the host's action isn't random. He knows where the car is and deliberately opens a door that does not contain it. This biases the outcome in favor of switching—no matter how you combine or recombine the probabilities in your head.

Our tendency to segment—Door 1 + Door 2, or Door 1 + Door 3—can lead to conflicting strategies. From one perspective, switching seems optimal. From another, staying appears defensible. But these fragmented views obscure the underlying constant: the original choice always has just a 1/3 chance of being correct.

Generalizing the Problem: Three Choices, One Truth

Let’s test this with all three possible initial choices:

· If you choose Door 1 (car is behind it), switching loses.

· If you choose Door 2 (car is behind Door 1), switching wins.

· If you choose Door 3 (car is behind Door 1), switching again wins.

In two out of three cases, switching gets you the car. That’s the statistical heart of the problem. Any mental gymnastics about which doors "contain" 2/3 of the probability don’t change this basic reality. Segmenting the doors into abstract groupings might seem logical, but it only muddles the simple structure of the game.

What This Reveals About the Mind

The Monty Hall problem reveals something larger than a quirk of game theory. It shows how the intellect—so skilled at building complex frameworks—often leads us astray when we overlook the simplicity of empirical facts. Even with clear rules, we construct elaborate rationalizations that feel right but are statistically wrong.

This isn’t just about games. In everyday life, we often overthink and oversegment—applying the intellect where direct observation and simplicity would serve us better. As with the Monty Hall problem, the truth is often hidden behind the clutter of our own reasoning.

So, what’s the takeaway? Choose simplicity. Let the numbers speak. Observe carefully. And in the face of overthinking, remember: sometimes, switching doors really is the smarter move.

Want to explore the probabilities yourself?
Try this interactive simulation: https://www.mathwarehouse.com/monty-hall-simulation-online/